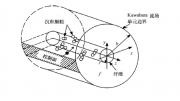
Kuwabara單纖維過濾模型用于分析纖維過濾介質表面塵粒捕集問題。如圖 1所示, 圓柱纖維體垂直氣流方向置于 Kuwabara流場單元的中心, 在控制面上隨機釋放的粒子受流體 Stokes拖拽力、重力及電場力等作用下被輸送至纖維過濾介質表面附近, 因粒子與纖維表面間的范德華力而被捕集。此時, 被捕集的粒子作為新的捕集體對隨后的來流粒子具有捕集作用。隨著過濾過程的進行, 塵粒不斷被捕集形成鏈狀堆積結構, 即“粉塵樹枝”結構, 引起纖維捕集效率的增加。在忽略外力場作用和粒子的布朗運動情形下,粒子僅受到流體的拖拽力, 因此將(1)式轉化為圖 1坐標系下空間對時間的變換規律后, 得到粒子運動軌跡方程為式中 τ為粒子運動的速度松弛時間, s;mp為粒子質量, kg;ux、uy為氣流繞纖維的流動速度, m/s。該速度可由 Kuwabara流表示, 由文獻 [ 6] 給出的 Ku-wabara流在極坐標下表示為式中 ur為徑向速度, m/s;r為徑向坐標, m;θ為極角坐標, rad;uθ為橫向速度, m/s;c表示單纖維過濾模型的填充密度, c=(rf/b)2 ;rf為纖維半徑, m;b為Kuwabara流場單元的半徑, m;u0 為主流平均速度, m/ ,s(u0 =u∞ /(1 -c), u∞為未受干擾的來流速度,亦稱過濾風速, 下同);Ku為 Kuwabara動力學因子,在圖 1所示的直角坐標下, Kuwabara流速度可由以下關系獲得dT2式中 St為表征粒子慣性的 Stokes數, 定義為 St= ρpu∞ d2pCm /18μrf;ρp為粒子密度, kg/m3 ;dp為粒子直徑, m;μ為空氣動力粘度, kg/m· s;Cm為粒子的肯寧漢滑移修正因子;其余各量定義見圖 1。考慮到粒子在氣流中隨機分布特征, 將粒子運動的起始點隨機置于圖 1中的控制面上, 并進一步假設粒子的初始速度與粒子所在位置處流體速度相當考慮已捕集粒子對隨后來流粒子捕集的影響時, 由已捕集粒子和纖維體構成的捕集體對粒子的捕集共同起作用, 捕集體形狀因粒子的捕集而不斷發生變化, 因此, 基于極限軌跡的單纖維捕集效率計算方法已不再適應。令 t時間內通過控制面的粒子數為 MG, 其中, 被捕集的粒子數為 MC, 并假設氣流中粒子數濃度為 Cn, 個/m3 , 則如前所述, 本文討論粒子直徑 dp≥0.5 μm的情形, 并忽略其他外力場作用, 因此, 粒子捕集機制為攔截效應和慣性碰撞。在數值求解粒子運動軌跡時, 粒子運動時間步長為 Δt=0.01 ～ 0.05, 其中小粒子取下限, 大粒子取上限。計算所需基本參數按如下條件規定:空氣動力粘度取 1.8192 ×10-5 kg/(m· s);單纖維過濾模型的填充密度分別為 0.01、0.03和 0.05;粒子直徑取為 0.5、1和 1.5 μm, 纖維直徑為 10 μm;纖維長度為 50 μm。由于氣流中粒子分布的隨機特征, 每次模擬結果為一次隨機事件, 因此, 在相同計算條件下執行多次模擬結果的平均才具有統計意義, 在本文的計算中, 每種計算條件下執圖 2顯示的是典型的單纖維過濾介質表面的粒子捕集過程。從圖 2中可以看出, 粒子在過濾介質表面的捕集過程可分為 3 個典型的階段, 分別為初始捕集階段、纖維-樹枝捕集階段和完全樹枝捕集階段。當過濾介質處于清潔狀態時, 粒子被過濾介質直接捕集, 捕集效率增加緩慢, 這一階段稱之為初始捕集階段或穩態過濾階段。隨著過濾介質上捕集的粒子數增多, 開始有粉塵樹枝生成, 此時一部分粒子被過濾介質捕集, 而另一部分粒子則被已捕集的粒子捕集, 捕集效率迅速增加, 這一階段稱之為纖維-樹枝捕集階段。隨著粉塵樹枝進一步長大, 絕大部分粒子被粉塵樹枝捕集, 系統進入“塵濾塵”階段,也即完全樹枝捕集階段。粒子在單纖維過濾介質表面捕集呈現的 3個階段對應于實際過濾中 3個典型的過濾階段, 即穩態過濾階段、過渡過濾階段和濾餅圖 3給出的是不同 St數下的粉塵樹枝結構。模擬計算所取參數如下:粒子直徑 dp =1 μm, 單纖維過濾模型填充密度 c=0.03, St數分別取為 2.47、 0.62和 0.06。通過改變粒子的密度和過濾風速取得相應的 St數值, 捕集的最大粒子數規定為800個。圖 3給出的是不同 St數下的粉塵樹枝結構。模擬計算所取參數如下:粒子直徑 dp =1 μm, 單纖維過濾模型填充密度 c=0.03, St數分別取為 2.47、 0.62和 0.06。通過改變粒子的密度和過濾風速取得相應的 St數值, 捕集的最大粒子數規定為800個。從圖 3中可以看出, St數對粉塵樹枝的形態影響明顯。當 St數較大時, 粒子捕集形成的粉塵樹枝結構不明顯, 只在沉積物上層出現細小的粉塵樹枝。粒子在沿 Z軸方向的分布也較為均勻, 這一結果與文獻[ 8]的實驗觀察結果一致(見圖 4(a));當 St數較小時, 粒子捕集形成的粉塵樹枝結構明顯, 沿 Z軸方向的分布極不均勻, 甚至在局部地方出現較大的粉塵絮團, 這一結果也同樣得到了實驗的證實粉塵樹枝的形態及粒子的分布依賴于 St數的原因是:在小 St數下, 纖維捕捉到粒子的概率小, 一旦有粒子在纖維上捕集, 則該點捕捉到粒子的概率數下, 粒子在纖維體附近的運動軌跡較彎曲, 形成的遮擋區域較大[ 10] , 從而在纖維表面形成分叉顯著的粉塵樹枝結構;相反, 在大 St數下, 纖維過濾介質上各點捕捉到粒子的概率較大, 粉塵樹枝的優勢生長減弱, 粒子在纖維體附近的運動軌跡也較平直, 形成的遮擋區域也就較小, 從而粒子捕集形成的粉塵樹枝結構不明顯。另外, 從圖 3中還可以看出, St數由 2.47變化到 0.62, 沉積物由緊密的堆積結構變化到分叉顯著的粉塵樹枝結構, 粒子的分布逐漸向纖維前駐點附近聚集。但 St數由 0.62變化到 0.06, 粒子分布又逐漸向纖維前駐點兩側分散。從中可看出, 粒子在纖維過濾介質表面的分布角度隨 St數增大經歷兩個階段性變化:起初, 粒子分布角度隨 St數減小而減小;隨后, 隨 St數減小而增大。本模擬中, 粒子在過濾介質表面的最小分布角度出現在 St=0.62。圖 5顯示的是單纖維過濾模型的填充密度分別為 0.01、0.03和 0.05時的粉塵樹枝形態。模擬計算所需參數規定為:粒子直徑為 1 μm, 粒子密度為1 g/cm3 , 過濾風速為 0.2 m/s。從圖 5中可以看出,填充密度為 0.01時, 粒子捕集形成的粉塵樹枝數目較少, 但單個樹枝結構尺度大;填充密度為 0.03和0.05兩種情形下的粉塵樹枝結構較為相似, 且粉塵樹枝沿 Z軸方向分布都較為均勻。圖 6所示的是 St數對捕集粒子數和單纖維捕集效率的影響。模擬計算中所需參數規定如下:粒子直徑取 1 μm, 單纖維過濾模型填充密度為 c= 0.03, St數分別為 0.12、1.5和 2.5, 最大捕集粒子數設為 800個。圖 6(a)給出的是不同 St數下捕集粒子數與釋放粒子數的關系曲線。其中橫坐標表示的是控制面上釋放的粒子數, 縱坐標表示的是捕集的粒子數。由式(13)可知, 釋放粒子數與過濾時間成比例, 因此, 圖 6(a)中橫坐標實質反映的是過濾時間。從圖 6(a)中可以看出, 捕集粒子數先隨釋放粒子數增加而呈緩慢增加, 且 St數越小, 緩慢增加的過程越長;隨著釋放粒子數的進一步增加, 捕集粒子數出現一個快速增加過程;此后, 捕集粒子數隨釋放粒子數呈近似線性增加關系, 且這種線性增加率在 3種 St數情形下也較為接近, 這說明 St數對粒子的捕集影響已大為減弱, 而粉塵樹枝對粒子的捕集圖 6(b)給出的是不同 St數下捕集粒子數對單纖維捕集效率的影響。橫坐標表示捕集粒子數, 縱坐標表示無量綱捕集效率(單纖維捕集效率與清潔纖維捕集效率之比)。不同 St數下清潔纖維捕集效率也表示在圖中, 從圖 6(b)可以看出, 在粒子捕集的初始階段, St數對粒子的捕集起決定作用, St數越大, 單纖維捕集效率越高, 這與經典纖維過濾理論的分析結果一致[ 11] 。隨著捕集粒子數的增多, 3種情形下, 單纖維捕集效率均呈線性增加, 但增加的幅度有所不同, St數越大, 單纖維捕集效率的增加幅度越小。在捕集粒子數為 800 個時, 3 種情形的單纖維捕集效率均達到 3.5%左右, 這進一步說明在粒子捕集的后期階段, 粉塵樹枝對粒子捕集起主導作用。